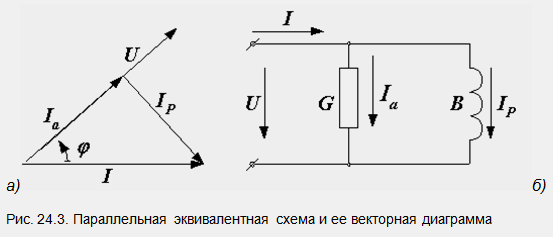
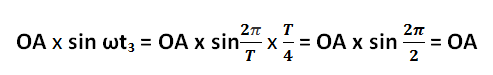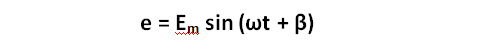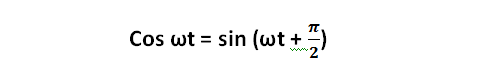Особенности синусоидального тока
Наиболее желательной формой кривой для мгновенных значений переменного тока и напряжения является синусоидальная форма.
Схема синусоидального тока.
В математике синусоидальные изменения считаются простейшей гармонической формой периодического процесса, поэтому расчет цепей синусоидального тока относительно прост и в таких цепях отсутствуют нежелательные побочные явления.
Рисунок 1. Построение синусоидальной кривой при помощи вращающего вектора.
Для построения синусоидальной кривой возьмем некоторый отрезок OA (рис. 1), длина которого в масштабе построения равна максимальному значению синусоидальной величины, — это вектор синусоидальной величины.
Например, Im = OA x n= 10 а, масштаб n = 0,1 а/мм; OA = 10 : 0,1 = 100 мм. В прямоугольной системе координат направим этот вектор сначала по горизонтальной оси — это будет исходное положение вектора в момент начала отсчета времени, т. е. при t = 0.
Вектор вращается с постоянной угловой скоростью против часовой стрелки. За время периода Т вектор поворачивается на 2? радиан (рад). Следовательно, его угловая скорость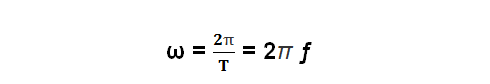
Так как в выражение ? входит частота переменного тока, то угловую скорость вектора обычно называют угловой частотой.
Когда с момента начала отсчета пройдет некоторое время t1 тогда вектор OA повернется на угол ?t1. Из конца вектора OA, находящегося в новом положении, опустим перпендикуляр на горизонтальную ось. Длина этого перпендикуляра будет OA x sin ?t1. В некоторый следующий момент t2 вектор образует с горизонтальной осью угол ?t2, а длина перпендикуляра, опущенного из его конца, будет, соответственно, OA хsin t2. Спустя четверть периода с момента начала отсчета времени, т. е. в момент t3 = T/4 вектор OA станет перпендикулярно к горизонтальной оси, а длина перпендикуляра
Рисунок 2. Синусоидальная величина с положительной начальной фазой.
Теперь рядом с окружностью, описываемой концом вращающегося вектора, построим в прямоугольной системе кривую зависимости величины OA х sin ?t от ?t или от t — это и будет синусоидальная кривая за промежуток времени от t = О до t = t3.
В момент t3 = T/4 синусоидальная величина достигает максимального значения. По мере дальнейшего вращения вектора величина OA х sin ?t убывает (моменты t4 и t5). Наконец, в момент t6 = T/2, описав дугу, равную ? радианам, вектор примет горизонтальное положение. В момент, когда OA х sin ?t6 = OA х sin ?=0“, синусоидальная величина проходит через нулевое значение.
При дальнейшем вращении вектора перпендикуляр OA х sin ?t будем считать отрицательным (моменты t7, ts, ts). Соответственно, построим вниз от горизонтальной оси этот участок синусоидальной кривой.
Если в начальный момент t = 0 вектор образует с горизонтальной осью некоторый угол а, то в момент начала отсчета синусоидальная величина не равна нулю, а имеет значение OA х sin 0 (рис. 2). Угол а называется начальным фазовым углом, или начальной фазой. В этом случае длина перпендикуляра, опущенного из конца вектора OA на горизонтальную ось в момент t, будет:
OA x sin (?t + a),
в соответствии с этим синусоидальная кривая в начальный момент не пройдет через нуль. Таким образом, в общем случае желательно, чтобы переменный ток изменялся во времени согласно выражению
i = Im x sin (?t + a).
В этом выражении i – мгновенное значение силы тока, Im — максимальное значение (амплитуда). Для получения синусоидального тока необходимо, чтобы ЭДС генераторов переменного тока была тоже синусоидальная,
здесь ? – произвольная начальная фаза этой ЭДС. Если ЭДС е и ток i, относящиеся к одной и той же цепи, неодновременно проходят через нулевое или максимальное значение, то они сдвинуты по фазе относительно друг друга (рис. 3). При наличии сдвига фаз ЭДС в цепи может быть равна нулю, а ток еще будет в ней проходить, или же ток может быть равен нулю при наличии значительной ЭДС,
Рисунок 3. Сдвиг фаз между э. д. с. и током.
Сдвиг фаз ф измеряется разностью начальных фаз синусоидальных величин. В рассматриваемом нами случае ф = ? – а, причем ЭДС опережает по фазе ток. Соответственно, векторы Em и Im образуют угол ф, который остается неизменным при их вращении.
Синусоидальные величины, например напряжение и ток, совпадают по фазе, если их начальные фазы одинаковы; они же противоположны по фазе, если их сдвиг фаз ф = ± ?. Если одна из синусоидальных величин изменяется по синусоиде, например i = Im x sin ?t, а вторая — по косинусоиде, например u = Um cos ?t, то сдвиг фаз между ними ф = ? /2 (чему соответствует четверть периода), так как
Необходимо иметь в виду, что вращающиеся векторы величин переменного тока существенно отличаются от векторов физических величин (силы, скорости, магнитной индукции, напряженности электрического поля и т. п.), имеющих определенное направление в пространстве.
Векторы переменного тока, называемые также радиус-векторами, представляют собой лишь удобную математическую форму изображения величин, изменяющихся во времени синусоидально. Радиус-векторы, как и пространственные векторы, часто кратко называют одинаково векторами. Векторы переменного тока отличают точкой над буквой, обозначающей ту или иную синусоидальную величину, например ?m или ?m
